浅谈Mysql的BTree
浅谈MySQL的BTREE索引
MySQL的MyISAM、InnoDB引擎默认均使用B+树索引(查询时都显示为“BTREE”),本文讨论两个问题:
- 为什么MySQL等主流数据库选择B+树的索引结构?
- 如何基于索引结构,理解常见的MySQL索引优化思路?
为什么索引无法全部装入内存
索引结构的选择基于这样一个性质:大数据量时,索引无法全部装入内存。
为什么索引无法全部装入内存?假设使用树结构组织索引,简单估算一下:
- 假设单个索引节点12B,1000w个数据行,unique索引,则叶子节点共占约100MB,整棵树最多200MB。
- 假设一行数据占用200B,则数据共占约2G。
假设索引存储在内存中。也就是说,每在物理盘上保存2G的数据,就要占用200MB的内存,*索引:数据的占用比约为1/10。1/10的占用比算不算大呢?物理盘比内存廉价的多,以一台内存16G硬盘1T的服务器为例,如果要存满1T的硬盘,至少需要100G的内存*,远大于16G。
考虑到一个表上可能有多个索引、联合索引、数据行占用更小等情况,实际的占用比通常大于1/10,某些时候能达到1/3。在基于索引的存储架构中,索引:数据的占用比过高,因此,索引无法全部装入内存。
其他结构的问题
由于无法装入内存,则必然依赖磁盘(或SSD)存储。而内存的读写速度是磁盘的成千上万倍(与具体实现有关),因此,核心问题是“如何减少磁盘读写次数”。
首先不考虑页表机制,假设每次读、写都直接穿透到磁盘,那么:
- 线性结构:读/写平均O(n)次
- 二叉搜索树(BST):读/写平均O(log2(n))次;如果树不平衡,则最差读/写O(n)次
- 自平衡二叉搜索树(AVL):在BST的基础上加入了自平衡算法,读/写最大O(log2(n))次
- 红黑树(RBT):另一种自平衡的查找树,读/写最大O(log2(n))次
BST、AVL、RBT很好的将读写次数从O(n)优化到O(log2(n));其中,AVL和RBT都比BST多了自平衡的功能,将读写次数降到最大O(log2(n))。
假设使用自增主键,则主键本身是有序的,树结构的读写次数能够优化到树高,树高越低读写次数越少;自平衡保证了树结构的稳定。如果想进一步优化,可以引入B树和B+树。
B树解决了什么问题
很多文章将B树误称为B-(减)树,这可能是对其英文名“B-Tree”的误解(更有甚者,将B树称为二叉树或二叉搜索树)。特别是与B+树一起讲的时候。想当然的认为有B+(加)树就有B-(减)树,实际上B+树的英文名是“B+-Tree”。
如果抛开维护操作,那么B树就像一棵“m叉搜索树”(m是子树的最大个数),时间复杂度为O(logm(n))。然而,B树设计了一种高效简单的维护操作,使B树的深度维持在约log(ceil(m/2))(n)~logm(n)之间,大大降低树高。
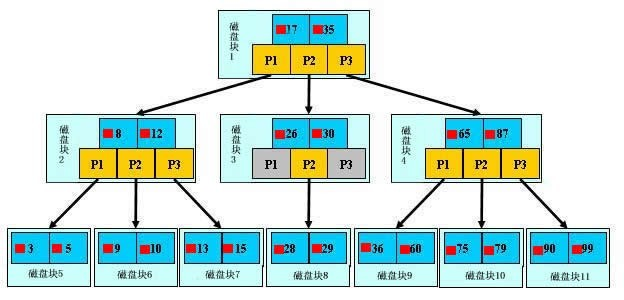
再次强调:
不要纠结于时间复杂度,与单纯的算法不同,磁盘IO次数才是更大的影响因素。读者可以推导看看,B树与AVL的时间复杂度是相同的,但由于B树的层数少,磁盘IO次数少,实践中B树的性能要优于AVL等二叉树。
同二叉搜索树类似,每个节点存储了多个key和子树,子树与key按顺序排列。
页表的目的是扩展内存+加速磁盘读写。一个页(Page)通常4K(等于磁盘数据块block的大小,见inode与block的分析),从磁盘读写的角度出发,操作系统每次以页为单位将内容从磁盘加载到内存(以摊分寻道成本),修改页后,再择期将该页写回磁盘。考虑到页表的良好性质,可以使每个节点的大小约等于一个页(使m非常大),这每次加载的一个页就能完整覆盖一个节点,以便选择下一层子树;对子树同理。对于页表来说,AVL(或RBT)相当于1个key+2个子树的B树,由于逻辑上相邻的节点,物理上通常不相邻,因此,读入一个4k页,页面内绝大部分空间都将是无效数据。
假设key、子树节点指针均占用4B,则B树节点最大m * (4 + 4) = 8m B;页面大小4KB。则m = 4 * 1024 / 8 = 512,一个512叉的B树,1000w的数据,深度最大 log(512/2)(10^7) = 3.02 ~= 4。对比二叉树如AVL的深度为log(2)(10^7) = 23.25 ~= 24,相差了5倍以上。震惊!B树索引深度竟然如此!
另外,B树对局部性原理非常友好。如果key比较小(比如上面4B的自增key),则除了页表的加成,缓存还能进一步预读加速。美滋滋~
B+树解决了什么问题
B树的剩余问题
然而,如果要实际应用到数据库的索引中,B树还有一些问题:
- 未定位数据行
- 无法处理范围查询
问题1
数据表的记录有多个字段,仅仅定位到主键是不够的,还需要定位到数据行。有3个方案解决:
- 直接将key对应的数据行(可能对应多行)存储在节点中。
- 数据行单独存储;节点中增加一个字段,定位key对应数据行的位置。
- 修改key与子树的判断逻辑,使子树大于等于上一key小于下一key,最终所有访问都将落于叶子节点;叶子节点中直接存储数据行或数据行的位置。
方案1中,数据行通常非常大,存储数据行将减少页面中的子树个数,m减小树高增大。假设数据行占用200B,可忽略组织B树的指针,则新的m = 4 * 1024 / 200 = 20.48 ~= 21,深度最大 log(21/2)(10^7) ~= 7。增加了一倍以上的IO,不考虑。
方案2中,节点增加了一个字段。假设是4B的指针,则新的m = 4 * 1024 / 12 = 341.33 ~= 341,深度最大 log(341/2)(10^7) = 3.14 ~= 4。与3差别不大,可以考虑。
方案3的节点m与深度不变,但时间复杂度变为稳定的O(logm(n))。考虑。
问题2
实际业务中,范围查询的频率非常高,B树只能定位到一个索引位置(可能对应多行),很难处理范围查询。给出2种方案:
- 不改动:查询的时候先查到左界,再查到右界,然后DFS(或BFS)遍历左界、右界之间的节点。
- 在“问题1-方案3”的基础上,由于所有数据行都存储在叶子节点,B树的叶子节点本身也是有序的,可以增加一个指针,指向当前叶子节点按主键顺序的下一叶子节点;查询时先查到左界,再查到右界,然后从左界到有界线性遍历。
乍一看感觉方案1比方案2好——时间复杂度和常数项都一样,方案1还不需要改动。但是别忘了局部性原理,不管节点中存储的是数据行还是数据行位置,方案2的好处在于,叶子节点连续存储,对页表和缓存友好。而方案1则面临节点逻辑相邻、物理分离的缺点。
引出B+树
综上,问题1的方案2与问题2的方案1可整合为一种方案(基于B树的索引),问题1的方案3与问题2的方案2可整合为一种(基于B+树的索引)。实际上,数据库、文件系统有些采用了B树,有些采用B+树。
包括MySQL在内的主流数据库多选择了B+树。即:
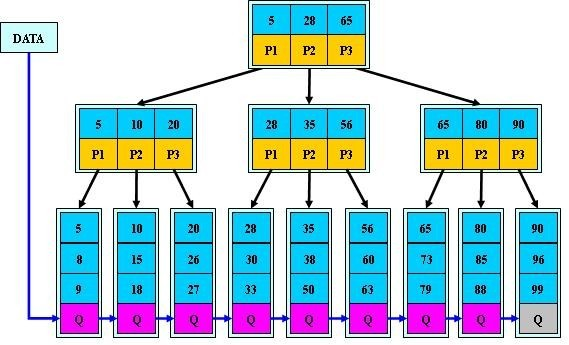
主要变动如上所述:
- 修改key与子树的组织逻辑,将索引访问都落到叶子节点
- 按顺序将叶子节点串起来(方便范围查询)
B树和B+树的增、删、查过程
B树的增删过程暂时可参考从B树、B+树、B*树谈到R 树的“6、B树的插入、删除操作”小节,B+树的增删同理。此处暂不赘述。
Mysql索引优化
根据B+树的性质,很容易理解各种常见的MySQL索引优化思路。
暂不考虑不同引擎之间的区别。
优先使用自增key作为主键
前面的分析中,假设用4B的自增key作为索引,则m可达到512,层高仅有3。使用自增的key有两个好处:
- 自增key一般为int等整数型,key比较紧凑,这样m可以非常大,而且索引占用空间小。最极端的例子,如果使用50B的varchar(包括长度),那么
m = 4 * 1024 / 54m = 75.85 ~= 76,深度最大log(76/2)(10^7) = 4.43 ~= 5,再加上cache缺失、字符串比较的成本,时间成本增加较大。同时,key由4B增长到50B,整棵索引树的空间占用增长也是极为恐怖的(如果二级索引使用主键定位数据行,则空间增长更加严重)。 - 自增的性质使得新数据行的插入请求必然落到索引树的最右侧,发生节点分裂的频率较低,理想情况下,索引树可以达到“满”的状态。索引树满,一方面层高更低,一方面删除节点时发生节点合并的频率也较低。
最左前缀匹配
索引可以简单如一个列(a),也可以复杂如多个列(a, b, c, d),即联合索引。如果是联合索引,那么key也由多个列组成,同时,索引只能用于查找key是否存在(相等),遇到范围查询(>、<、between、like左匹配)等就不能进一步匹配了,后续退化为线性查找。因此,列的排列顺序决定了可命中索引的列数。
如有索引(a, b, c, d),查询条件a = 1 and b = 2 and c > 3 and d = 4,则会在每个节点依次命中a、b、c,无法命中d。也就是最左前缀匹配原则。
=、in自动优化顺序
不需要考虑=、in等的顺序,mysql会自动优化这些条件的顺序,以匹配尽可能多的索引列。
如有索引(a, b, c, d),查询条件c > 3 and b = 2 and a = 1 and d < 4与a = 1 and c > 3 and b = 2 and d < 4等顺序都是可以的,MySQL会自动优化为a = 1 and b = 2 and c > 3 and d < 4,依次命中a、b、c。
索引列不能参与计算
有索引列参与计算的查询条件对索引不友好(甚至无法使用索引),如from_unixtime(create_time) = '2014-05-29'。
原因很简单,如何在节点中查找到对应key?如果线性扫描,则每次都需要重新计算,成本太高;如果二分查找,则需要针对from_unixtime方法确定大小关系。
因此,索引列不能参与计算。上述from_unixtime(create_time) = '2014-05-29'语句应该写成create_time = unix_timestamp('2014-05-29')。
能扩展就不要新建索引
如果已有索引(a),想建立索引(a, b),尽量选择修改索引(a)为索引(a, b)。
新建索引的成本很容易理解。而基于索引(a)修改为索引(a, b)的话,MySQL可以直接在索引a的B+树上,经过分裂、合并等修改为索引(a, b)。
不需要建立前缀有包含关系的索引
如果已有索引(a, b),则不需要再建立索引(a),但是如果有必要,则仍然需考虑建立索引(b)。
选择区分度高的列作索引
很容易理解。如,用性别作索引,那么索引仅能将1000w行数据划分为两部分(如500w男,500w女),索引几乎无效。
区分度的公式是count(distinct <col>) / count(*),表示字段不重复的比例,比例越大区分度越好。唯一键的区分度是1,而一些状态、性别字段可能在大数据面前的区分度趋近于0。
这个值很难确定,一般需要join的字段要求是0.1以上,即平均1条扫描10条记录。
参考:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!